
To simulate a set of observations for this situation under the assumption that the mean number of cars that go by per hour is actually $52$, one can use: To generate $n$ realizations of a random variable that follows a Poisson distribution, counting the number of occurrences of some event within some well-defined interval or range, where the mean number of occurrences in that interval is expected to be $\lambda$.Īs an example, suppose over the course of 15 weeks, every Saturday - at the same time - an individual stands by the side of a road and tallies the number of cars going by within a 120-minute window. Simulating Random Variables following Poisson Distributions This function can be found by making the following menu selections:

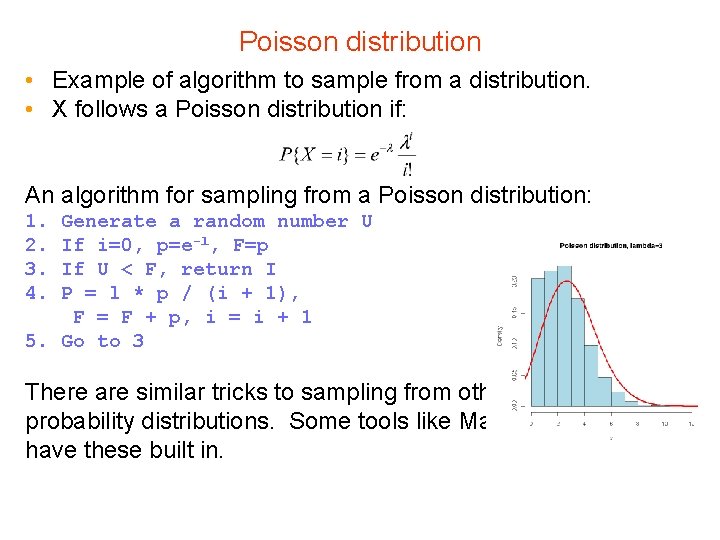
That is to say, it gives the sum $P(0) + P(1) + \cdots + P(k)$. The last argument for this function, when $TRUE$, indicates the probability returned should be cumulative. $$P(k) = \frac$$Īs an example, suppose that in a given call center that gets on average 13 calls every hour, one can calculate the probability that in a given $15$ minute period the call center will receive less than $6$ calls with the following: Suppose one wishes to find the Poisson probability of seeing exactly $k$ occurrences of some event within some well-defined interval, where the mean number of occurrences in that interval is expected to be $\lambda$.
Tech Tips: Poisson Distributions Calculating $P(X=x)$ when $X$ follows a Poisson Distribution


 0 kommentar(er)
0 kommentar(er)
